Category Archives: Matematica

La democrazia? Questione di matematica

Posted on by

Democrazia: La miglore forma di governo? Per rispondere a questa domanda non useremo la filosofia, la politica o la giurisprudenza, useremo l’unica disciplina che è “senza macula d’errore e certissima per se” (cit. Dante Alighieri): la matematica.

Supponiamo che l’elettorato sia composto da N individui che ragionano in modo del tutto indipendente. Devono scegliere un leader tra due possibilità.

Ciascuno di loro ha una probabilità di fare la scelta migliore (ammesso che esista) poco maggiore del 50 % (ad esempio il 50 + \varepsilon %). Qual è la probabilità che la maggioranza della popolazione scelga il miglior leader?

Se la vostra risposta intuitiva è stata 50 + \varepsilon % avete sbagliato di grosso. Infatti si può dimostrare con un facile calcolo combinatorio che la probabilità di avere esito positivo alle elezioni cresce vertiginosamente all’aumentare degli elettori.
Anche se la probabilità \varepsilon di riconoscere la scelta migliore da quella sbagliata per ciascun elettore fosse bassissima, ad esempio dello 0.05 %, il numero di elettori necessari ad avere più del 99.9 % di probabilità che l’esisto della votazione vada a buon fine è di 25 milioni.

\displaystyle 2\varepsilon \sqrt N > 5\qquad \Longrightarrow \qquad N > \frac{6.25}{\varepsilon^2}

In Italia siamo circa 60 milioni, se tutti ragionassimo con la propria testa, avremmo la certezza assoluta di eleggere sempre il miglior leader possibile.

Se ammettiamo tuttavia che la classe dirigente italiana non è poi la migliore possibile ci deve essere un problema da qualche parte. Nel conto precedente abbiamo supposto che i voti degli elettori siano tutti indipendenti tra loro.
Nella realtà questo non è vero, il voto di ciascun individuo è fortemente influenzato dall’ambiente che lo circonda.

Un elettore circondato da persone della stessa idea politica è più probabile che l’abbracci dando il proprio voto dello stesso colore politico dei suoi amici o familiari, piuttosto che compiere la scelta in maniera indipendente.

Costruiamo una simulazione in cui ciascun individuo è connesso all’interno di una rete di comunicazione con gli altri. La rete usata si chiama scale-free, ed è una buona schematizzazione delle relazioni umane, dove un limitato numero di persone ha molte connessioni con altri individui (vip, personaggi noti, politici, …) mentre la maggioranza possiede un numero ristretto di legami.

Ridefiniamo la probabilità che un individuo faccia la scelta corretta in questo modo:

\displaystyle p = \frac{1}{2} + \varepsilon + \left(\frac{1}{2} - \varepsilon\right)\frac{n^+ - n^-}{N_{joints}}

Dove n^+ e n^- rappresentano rispettivamente il numero di connessioni di quell’individuo con persone che hanno già scelto chi votare, N_{joint} il numero totale di connessioni di quell’individuo.

Lo straordinario risultato che avevamo ottenuto nel caso di elettori indipendenti è dovuto principalmente al fatto che mediare la votazione su un numero molto alto di elettori abbatte le fluttuazioni statistiche, permettendo a quel \varepsilon sopra al 50 % di essere determinante sull’esito della votazione (anche quando questo è solo dello 0.05 %).

Se confrontiamo le fluttuazioni statistiche nel caso di elettori indipendenti a quello di elettori dipendenti otteniamo una brutta sorpresa.

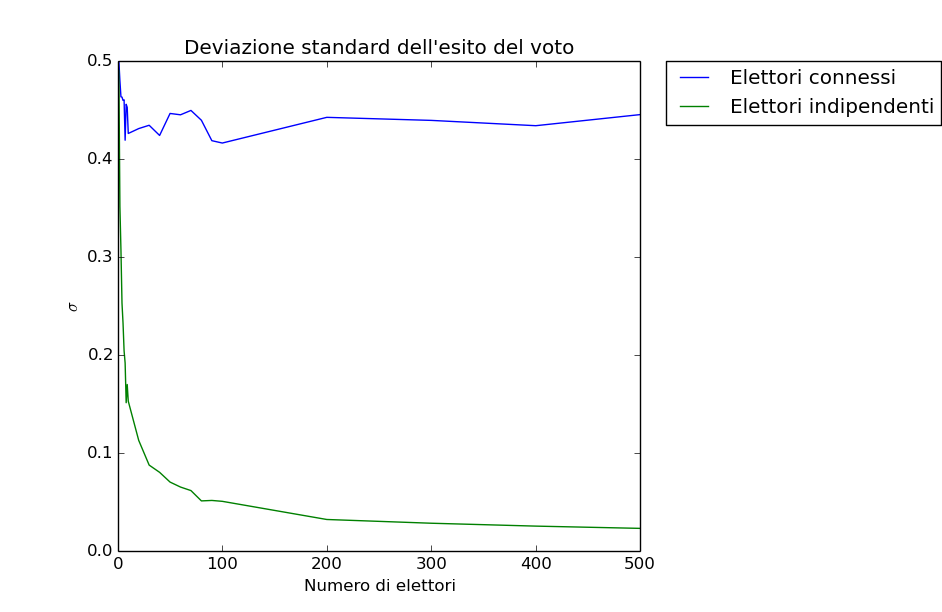
Nel grafico seguente è riportata la fluttuazione statistica (deviazione standard) del voto in funzione del numero di elettori in entrambi i casi:

Deviazione standard

Dalla figura si evince bene come nel caso di elettori indipendenti la deviazione standard decresce (come 1 / \sqrt{N}) all’aumentare del numero di elettori, migliorando l’esito della votazione.

Il caso di elettori reali  il risultato è disastroso, la deviazione standard non mostra alcuna diminuzione all’aumentare di N. Questo vuol dire chè le fluttuazioni statistiche sono molto più importanti in questo caso, rendendo molto più probabile, anche per alti valori di N, che la maggioranza degli elettori faccia la scelta sbagliata.

A questo fatto matematico può essere data una spiegazione qualitativa semplice: il primo  che compie la scelta influenzerà di conseguenza tutti gli elettori a cui e connesso, una scelta sbagliata all’inizio si ripercuote molto facilmente su tutti gli elettori che lo circondano, rendendo il risultato finale delle elezioni molto più incerto.

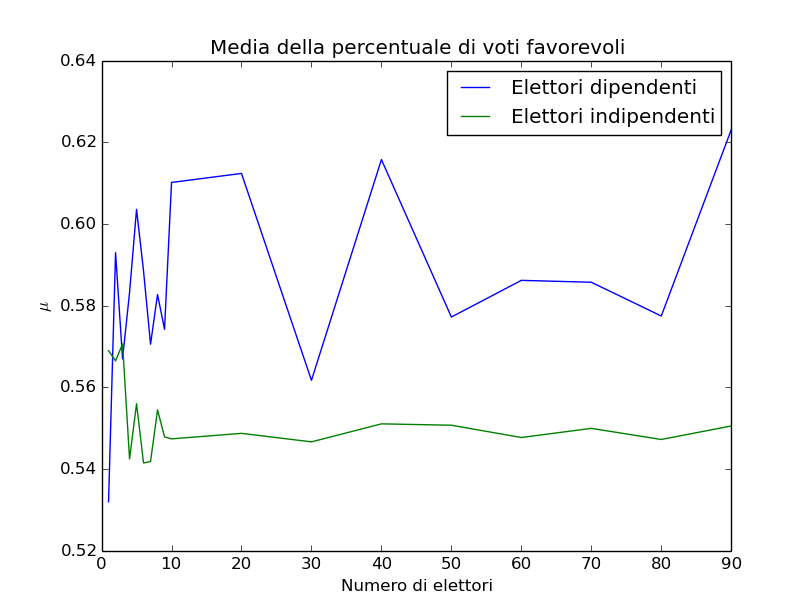
Tuttavia, poiché si ha quell’ \varepsilon di probabilità in più che gli elettori all’inizio riconoscano correttamente il migliore candidato, la decisione positiva si propaga con maggior facilità rispetto a quella negativa. Possiamo aspettarci che la percentuale di elettori media che compie la scelta giusta sia maggiore rispetto al caso di elettori indipendenti, come è mostrato nella seguente figura dove sono stati graficati i risultati della simulazione:

media2

Le grandi oscillazioni che mostra la linea blu sono dovute dalle grandi fluttuazioni statistiche che la simulazione con elettori reali mostra rispetto alla riga verde (meno frastagliata).

Si nota chiaramente che la linea blu (elettori connessi) ha un valore medio ben sopra il 55 % (valore usato nella simulazione) che è invece il valore attorno a cui oscilla il campione indipendente.

Come si compensano questi due effetti?
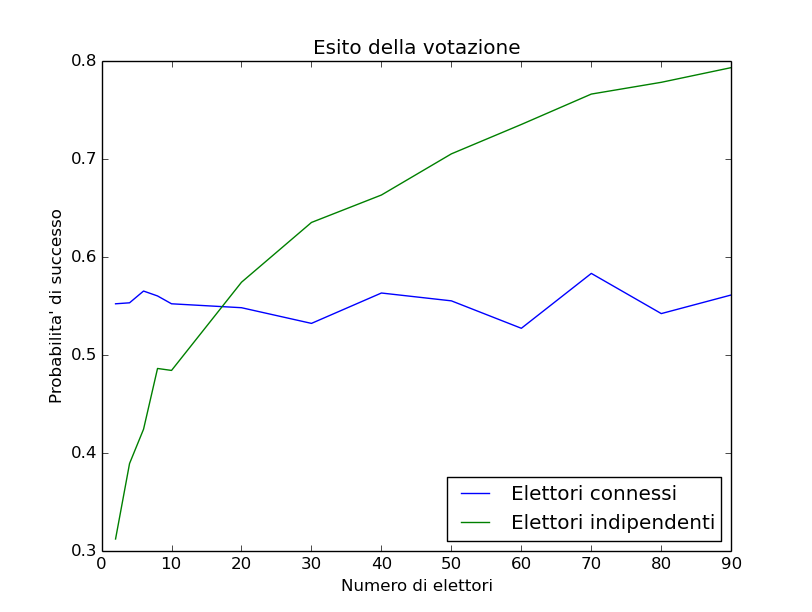
Il grafico seguente mostra la probabilità che la maggioranza degli elettori scelga bene.

ProbabilitaFinale

L’esito della votazione è quasi indipendente dal numero di elettori nella simulazione che tiene conto delle interazioni, mentre cresce vertiginosamente nel caso di elettori indipendenti.

Come si vede tra i 10 e i 20 elettori vi è la transizione di quale metodo è il migliore.

Questi modelli possono essere applicati anche alla formazione di collegi giudicanti quali giurie, commissioni d’esame o gruppi di lavoro.

In altri termini se abbiamo una piccola commissione (composta da meno di 10 elementi) il fatto che possano confrontarsi favorisce l’esito della scelta migliore. Viceversa se la commissione è grande (circa 20 persone) è molto più conveniente far emettere a ciascuna persona un giudizio singolo, senza dare possibilità di confronto, ed infine unire tutti i risultati.

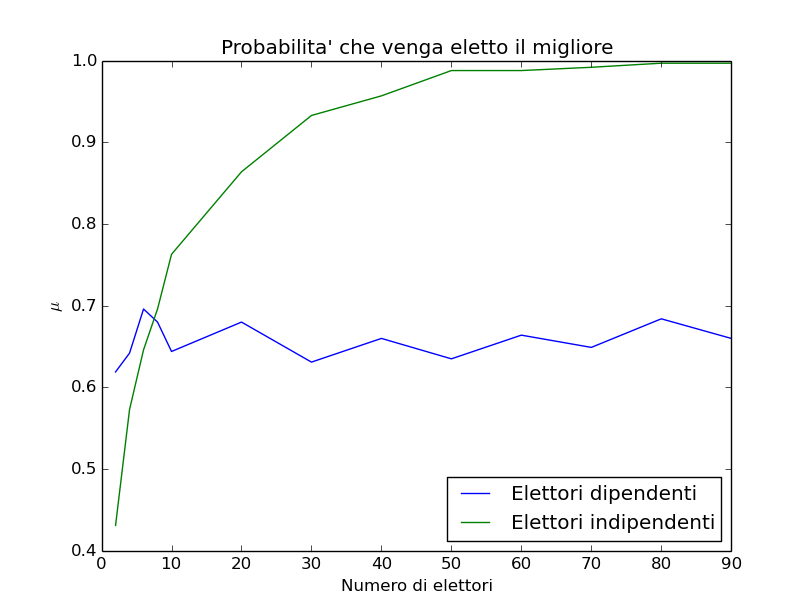
Tutta questa analisi è stata condotta con un valore di \varepsilon del 5 %. Se questo valore aumenta il numero N di persone a cui avviene il sorpasso del metodo indipendente è ancora più basso, come dimostra il grafico seguente, simulato con \varepsilon del 15 % (La probabilità che ciascun elettore facesse la migliore scelta è del 50 + 15 = 65 %)

ProbabilitaFinale2

Per gruppi piccoli, 3 o 4 persone, la collaborazione è costruttiva, ma appena il numero dei componenti aumenta la collaborazione diventa infruttuosa.

È matematicamente vero che “chi fa da se, fa per tre”.

(Per chi volesse approfondire i conti matematici una versione più dettagliata può essere scaricata da questo link: Versione Completa )

Lotta per la sopravvivenza

Posted on by

Il ciclo della vita.

La dinamica degli ecosistemi è uno degli argomenti più interessanti, in cui la fisica può essere applicata con successo per studiare l’evoluzione delle popolazioni di prede e predatori.

 

Supponiamo che nel nostro ecosistema ci siano solo due specie in lotta per la sopravvivenza: i pesci (le prede) e gli squali (i predatori).

I pesci hanno a disposizione risorse di cibo praticamente illimitate, se lasciate proliferare si moltiplicano molto rapidamente.

Viceversa gli scquali si cibano solo di pesci, la loro fonte di cibo è quindi molto più scarseggiante, e una sovrappopolazione di predatori causera la loro estinzione per mancanza di cibo. Con una simpatica simulazione è possibile visualizzare la dinamica.

In questa simulazione i quadratini verdi rappresentano i pesci, che si moltiplicano rapidamente, in rosso gli squali, se mangiano pesci si riproducono, altrimenti muoino. Ecco qui un video simpatico che mostra questo ecosistema in azione:

Come si può osservare in numero di pesci e squali aumenta e dinimuisce periodicamente. Se riportiamo su un grafico il numero di prede e quello di predatori notiamo molto bene questo comportamento:

 

Prede e predatori

Prede e predatori

La fisica può descrivere questo tipo di ecosistemi? Si!
Il numero di pesci all’interno del reticolo lo indichiamo con n, il numero di scquali con u.

Scriviamo un’equazione che descriva il comportamento medio di squali e pesci: la probabilità di un pesce di generare un figlio è costante (\alpha), mentre la probabilità che venga mangiata è proporzionale alla probabilità che nei paraggi ci sia uno squalo (\beta).

 
\displaystyle \dot n = n\left(\alpha - \beta u\right)
 
Allo stesso modo la probabilità di uno squalo di generare un figlio è tanto maggiore quanto più alta è la probabilità di incrociare un pesce (\gamma), ma hanno una probabilità costante di morire (\delta):

\displaystyle \dot u = u\left(\gamma n - \delta\right)
 
Queste equazioni (dette di Lotka-Volterra in onore dei due matematici che le formularono per primi) non hanno soluzione analitica, tuttavia con un cambio di variabili possiamo riscriverle in modo da poterne dare un’interpretazione fisica:
 
\displaystyle p = \ln n \qquad q = \ln u

\displaystyle \dot p = \frac{\dot n}{n} \qquad \dot q = \frac{\dot u}{u}
 

Con questa sostituzione il sistema di equazioni che descrive il comportamento medio dei nostri “pesciolini” è:
 
\displaystyle \left\{\begin{array}{l} \dot p = \alpha - \beta e^q \\ \dot q = \gamma e^p - \delta \end{array}\right.
 

Queste due equazioni differenziali adesso descrivono un sistema hamiltoniano canonico:
 
\displaystyle \left\{\begin{array}{l} \displaystyle \dot p = -\frac{\partial H}{\partial q}\\ \\ \displaystyle \dot q = \frac{\partial H}{\partial p} \end{array}\right.
 

Si può facilmente ricavare l’hamiltoniana di questo sistema:
 
\displaystyle H = -\alpha q -\delta p + \beta e^q + \gamma e^p
 

Quindi è possibile definire un “energia” dell’ecosistema, che è in media conservata (ricordiamoci che le equazioni che abbiamo scritto valgono in media, non tengono conto di piccole fluttuazioni locali della popolazione).
Risostituendo le variabili originali otteniamo che l’energia del sistema é:
 
\displaystyle H = \beta u + \gamma n - \alpha \ln u - \delta \ln n
 
Se il numero di pesci e squali è molto alto questo implica che la loro somma, pesata sui coefficienti \beta e \gamma si conserva.

\beta era la probabilità che, data un interazione tra preda e predatore, la preda muoia, mentre \gamma è la probabilità che, data un’interazione tra predatore abbia il sopravvento e quanto questa interazione sia favorevole alla sua procreazione.

Se dividiamo tutto per \beta otteniamo:
\displaystyle H' \approx u + \frac{\gamma}{\beta} n

Dove adesso \frac{\gamma}{\beta} è un coefficiente che tiene conto di quanto influenza il cibarsi dei predatori sulla loro crescita. La condizione \gamma = \beta vuol dire che ogni volta che un predatore acchiappa la preda, fa anche un figlio.

Questa condizione tuttavia è molto difficile da raggiungere in pratica, ecco la stima dei parametri per
una delle simulazioni effettuate:
 

\displaystyle \omega = \frac{\gamma}{\beta} \qquad \xi = \frac{\alpha}{\beta} \qquad \zeta = \frac{\delta}{\beta}
 

I valori ottenuti numericamente dalla simulazione sono:
\displaystyle \omega \approx 0.29 \qquad \xi \approx 0.36 \qquad \zeta \approx 0.069

Come si può vedere il modello di Lotka-Volterra descrive molto bene l’andamento che è stato misurato.
Conservazione

Oscillatore superarmonico

Posted on by

DomandaCosa hanno in comune un bambino che gioca sull’altalena, una molecola di ossigeno e un matto che fa Bungee Jumping?

Tutti e tre oscillano. La capacità di un sistema fisico di oscillare è una caratteristica molto comune. Ciascuno dei tre esempi risente di forze molto diverse tra loro.
L’altalena del bambino si muove grazie alla forza peso e alla reazione vincolare della catena a cui è sospesa, la molecola di ossigeno vibra a causa del legame coovalente che unisce i due atomi, e il matto che si butta da un ponte con il suo elastico da Bungee Jumping oscilla sotto l’azione combinata della forza di gravità e l’elastico a cui è appeso.

Quando le oscillazioni sono abbastanza piccole, una sola legge fisica accomuna tutti questi moti così diversi tra loro: l’oscillatore armonico. Qualche scienziato afferma addirittura che tutta la fisica si possa ricondurre all’oscillatore armonico.

 

Ma è davvero così?

 

Esaminiamo una forza di richiamo super elastica, di tipo:
\displaystyle F = -kx^3

Dalla seconda legge della dinamica possiamo ricavare un’equazione che descrive correttamente il moto di un punto materiale soggetto a questa forza:
\displaystyle F = ma = -kx^3

\displaystyle m\ddot x = -kx^3

Dove con \ddot x abbiamo indicato la derivata seconda della posizione fatta rispetto al tempo due volte.

Questa equazione differenziale non ammette soluzione analitica. Questa forza è conservativa, e l’energia potenziale è:
\displaystyle V(x) = \frac{1}{4} k x^4

Il profilo è mostrato in questa figura:

PotenzialeSuperarmonico

 

Se proviamo ad approssimare questo profilo con un potenziale armonico otteniamo una spiacevole sorpresa. Infatti il potenziale superarmonico non è approssimabile con nessun polininomio apparte se stesso. Questo è un esempio di sistema fisico oscillante che non è riconducibile ad un oscillatore armonico!

Non solo non siamo in grado di risolvere l’equazione differenziale che lo definisce, ma per questo potenziale è impossibile tentare un qualsiasi approccio di tipo perturbativo, poiché il più piccolo termine perturbativo non nullo è l’intera forza.

Ci dobbiamo arrendere di fronte a tali difficoltà? Siccome siamo fisici e non matematici, possiamo sfruttare le proprietà fisiche di questo sistema per capirci qualcosa.

Sappiamo che la soluzione di questo potenziale sarà un oscillatore, e vogliamo chiederci quale sia il suo periodo. In generale questo sarà funzione degli unici parametri che compaiono nell’equazione differenziale, e delle condizioni inziali, che qui riassumiamo nella variabile x_0 che rappresenta l’ampiezza di oscillazione:
\displaystyle T = f(m, k, x_0)

Questa funzione la possiamo spezzare in due parti, una che determinerà la dimensione fisica del periodo (i secondi) e una adimensionale che dipenderà dal dettaglio matematico della soluzione:
\displaystyle T = m^\alpha k^\beta x_0^\gamma C(m, k, x_0)

Dall’equazione differenziale di partenza possiamo ottenere le dimensioni dei parametri:
\displaystyle m = [Kg] \qquad k = [\frac{N}{m^3}] = [\frac{Kg}{m^2 s}] \qquad x_0 = [m]

Imponiamo che il periodo di oscillazione si misuri in secondi:

\displaystyle [s] = [Kg]^\alpha [\frac{Kg}{m^2 s^2}]^\beta [m]^\gamma

Da cui otteniamo il sistema per i coefficienti:

\displaystyle\left\{\begin{array}{l} \alpha + \beta = 0 \\ -2\beta + \gamma = 0 \\ -2\beta = 1 \end{array}\right.

Che può essere risolto facilmente:

\displaystyle \beta = -\frac{1}{2} \qquad \alpha = \frac{1}{2} \qquad \gamma = -1

Da cui abbiamo trovato la dipendenza dimensionale per il periodo:

\displaystyle T = \frac{1}{x_0}\sqrt{\frac{m}{k}} C(m, k, x_0)

Perché il termine adimensionale sia realmente funzione di quei parametri occorre che ci sia un modo per combinarli in modo da ottenere un risultato adimensionale. Ripetiamo quindi questa prova:

\displaystyle0 = [Kg]^\alpha [\frac{Kg}{m^2 s^2}]^\beta [m]^\gamma

Da cui otteniamo il sistema:

\displaystyle\left\{\begin{array}{l} \alpha + \beta = 0 \\ -2\beta + \gamma = 0 \\ -2\beta = 0 \end{array}\right.

Questo sistema ammette solo la soluzione:
\displaystyle\alpha = 0 \qquad \beta = 0 \qquad \gamma = 0

Abbiamo dimostrato che il termine C non può dipendere da nessun parametro, è quindi una costante. Da sole considerazioni di tipo dimensionale abbiamo ricavato la formula del periodo dell’oscillatore superarmonico, senza sapere nulla sulla soluzione matematica!

\displaystyle T = C\frac{1}{x_0}\sqrt{\frac{m}{k}}

Adesso il valore numerico di C può essere valutato risolvendo numericamente l’equazione differenziale con qualunque set di parametri iniziale e valutando il periodo numericamente.

Riportiamo in figura la soluzione numerica:

IntegrazioneNumericaDa cui si ottiene una stima di C pari a:

\displaystyle C \approx 7.42

Dalla figura dell’integrale numerico si vede che rispetto al moto armonico i potenziali superarmonici tendono ad avere una traiettoria più spigolosa, che assomiglia ad un segnale triangolare. Questo perché la potenza superarmonica tende ad appiattire il potenziale (n pari):
\displaystyle V = \frac{1}{n}kx^{n}\qquad \stackrel{n \rightarrow \infty}{\longrightarrow}\qquad \left\{\begin{array}{lr} \infty & x < -x_0 \mbox{ o } x > x_0 \\ 0 & x \in [-x_0,x_0] \end{array}\right.

Il potenziale assomiglia sempre più ad una buca infinita per n che cresce. All’interno della buca l’oggetto non è più soggetto a forze e tenderà a muoversi di moto rettilineo uniforme, e rimbalzando sulle pareti.

Possiamo calcolare facilmente il periodo per n \rightarrow \infty. Calcoliamo la velocità a cui si muove dentro la buca:
\displaystyle\frac{1}{2}mv^2 = \frac{1}{n}kx_0^{n}

\displaystyle v = \sqrt{\frac{2k x_0^n}{n m}} \qquad T= \frac{4x_0}{v}

Calcoliamo il periodo usando la legge del moto rettilineo uniforme:

\displaystyle T \stackrel{n\rightarrow\infty}{\longrightarrow} 4 \sqrt{\frac{nm}{2k}} x_0^{1 - \frac{n}{2}}

Per il caso che abbiamo trattato (n=4) la costante C approssimata ha un valore di 5.66, neanche troppo distante dal valore reale pari a 7.4. Questo è uno sviluppo corretto per grandi valori di n.

Ad esempio per n = 50 il valore di C stimato da questa relazione è 20.0, quello reale è 20.5. Riportiamo in figura il risultato dell’integrazione per n = 50:

PotenzialeTriangolare

 

Esiste un altro modo interessante per ottenere un espressione analitica di C nel caso n = 4.
Sfruttiamo la conservazione dell’energia meccanica:

\displaystyle\frac{1}{2}mv^2 + \frac{1}{4}kx^4 = E \displaystyle v = \sqrt{\frac{2}{m}\left(E - \frac{1}{4}kx^4\right)}

Questa è un altra equazione differenziale. Se ricordiamo che mezzo periodo è il tempo che il nostro oscillatore impiega per spostarsi dalla posizione -x_0 alla posizione x_0 possiamo integrare tutto quanto e ottenere:

\displaystyle\int_{x_0}^{-x_0} \frac{dx}{\sqrt{\frac{2}{m}\left(E - \frac{1}{4}kx^4\right)}} = \int_0^{\frac{T}{2}}dt \displaystyle \frac{T}{2} = \sqrt{\frac{m}{2}}\int_{-x_0}^{x_0} \frac{dx}{\sqrt{E - \frac{1}{4}kx^4}}

Ora l’energia totale E del sistema è pari all’energia potenziale superarmonica che l’oscillatore ha nel punto di massima ampiezza:

\displaystyle E = \frac{1}{4}kx_0^4

 

\displaystyle T = 2\sqrt{\frac{m}{2}}\frac{2}{x_0^2\sqrt{k}}\int_{-x_0}^{x_0} \frac{dx}{\sqrt{1 - \left(\frac{x}{x_0}\right)^4}}

Per rendere adimensionale l’integrale e ricavare il parametro C dobbiamo effettuare il seguente cambiamento di variabili per l’integrale

\displaystyle \xi = \frac{x}{x_0} \qquad dx = x_0d\xi

 

\displaystyle T = \frac{1}{x_0}\sqrt{\frac{m}{k}}\sqrt{8} \int_{-1}^1 \frac{d\xi}{\sqrt{1 - \xi^4}}

 

Abbiamo trovato un’espressione analitica per il termine C costante adimensionale nell’espressione del periodo:

\displaystyle T = \frac{1}{x_0}\sqrt{\frac{m}{k}} C

Questo termine può essere integrato numericamente:

\displaystyle C = \sqrt{8} \int_{-1}^1 \frac{d\xi}{\sqrt{1 - \xi^4}} \approx 7.42

In accordo con quanto ricavato risolvendo numericamente l’equazione differenziale.

 

 

 

Corsa sotto l’acquazzone

Posted on by

Quante volte ti è capitato di trovarti per strada senza ombrello mentre scoppia un acquazzone? Ti sei mai chiesto a che velocità conviene correre per bagnarsi il meno possibile?
Da un lato se cammini l’acqua ti colpisce solo in testa, per cui prendi meno goccie, se corri invece ti si bagna tutto il corpo, d’altra parte correre riduce il tempo in cui ti trovi sotto la pioggia…
Cosa conviene fare?
Con qualche semplice calcolo di fisica possiamo rispondere a questa domanda:

Volgiamo calcolare quanto si bagna un corpo che si muove con velocità v sotto la pioggia.
Chiamiamo \Phi il flusso di acqua che cade dal cielo, t il tempo che restiamo in balia della pioggia e \Sigma la superficie del nostro corpo esposta alle goccie d’acqua, il volume d’acqua che ci colpirà durante l’attraversata sarà:
B = \Phi\Sigma t
Il tempo t che restiamo sotto la pioggia possiamo calcolarlo con la legge del moto rettilineo uniforme:
t = \frac d v
Dove d è la distanza che ci separa dalla meta. La superficie esposta del nostro corpo dipende dall’angolo con cui le goccie
cadono:
\Sigma = S_c\sin\theta + S_t\cos\theta
Come si vede dalla figura seguente:

Pioggia

Dove S_c è la superficie della parte frontale del nostro corpo, S_t è la superficie della testa, vista dall’alto,
approssimiamo S_c \gg S_t.

Anche il flusso d’acqua tuttavia ha una dipendenza dalla nostra velocità: infatti se immaginiamo di volare verso la pioggia in alto,  la quantità d’acqua che ci urterà a parità di tempo sarà maggiore rispetto ad un osservatore fermo. Quindi esplicitiamo meglio il flusso di pioggia in funzione della velocità delle goccioline:

\Phi = n \frac{4}{3}\pi r^3 v_p
Dove n è la densità delle goccie di pioggia per unità di volume, r è il raggio della goccia di pioggia e vp è la velocità di caduta delle goccioline, se volgiamo il nuovo flusso di pioggia quando corriamo sotto la pioggia, otteniamo:
\Phi' = \Phi \frac {v'}{v_p}
Dove v’ è la velocità della pioggia nel nostro sistema di riferimento. Siccome non siamo in uno space shuttle per trovare v’ bastano
le trasformazioni di Galileo:
v' = \sqrt{v^2 + v_p^2}
\Phi' = \Phi\sqrt{1 + \frac {v^2}{v_p^2}}

Unendo tutto otteniamo:
B = \Phi\sqrt {1 + \frac{v^2}{v_p^2}}\frac d v \left(S_c\sin\theta + S_t\cos\theta\right)
Esplicitiamo la dipendenza di \theta dalla velocità v della persona:
\sin\theta = \frac{v}{\sqrt{v^2 + v_p^2}} \qquad \cos\theta = \frac{v_p}{\sqrt{v^2 + v_p^2}}

B = \Phi\sqrt{1 + \frac{v^2}{v_p^2}}\frac d v \frac{S_cv + S_t v_p}{\sqrt{v^2 + v_p^2}}

L’unico termine incognito è la velocità della goccia di pioggia. Questa in caduta libera nell’aria sarà soggetta a tre forze principali,
la forza peso che la spinge verso il basso, la forza di attrito viscoso che la rallenta e la forza di archimede. Il rapporto d’intensità
tra forza peso e forza di archimede è pari al rapporto tra densità dell’acqua e densità dell’aria, che per temperature tra zero e venti gradi
(temperature tipiche degli strati più bassi dell’atmosfera durante un acquazzone) è circa 1 su 1000, possiamo quindi tranquillamente ignorare
il contributo apportato dalla forza di archimende.

La velocità di regime si ottiene quindi uguagliando forza di attrito viscoso con la forza peso, supponendo laminare il moto delle goccie di pioggia nell’aria:
6\pi\eta r v_p = mg = \frac 4 3 \pi r^3 \rho_{H_2O}g
Da cui otteniamo:
v_p = \frac 2 9 \frac {\rho r^2 g}{\eta}
Il raggio di una goccia di pioggia dipende dal tipo di temporale, è varia in tra 0.1 mm (pioggerella lieve) e i 2 mm (Acquazzone pesante).

Tornando all’espressione per B (volume d’acqua che ci colpisce durante la nostra “passeggiata”), è conveniente esprimere tutto con il rapporto tra v e vp:
B = \Phi d \frac {v_p}{vv_p}\left(S_c\frac {v}{v_p} + S_t\right)
Definendo la variabile x
x = \frac {v}{v_p}

Si ottiene:
B = \frac{\Phi d}{v_p}\;\frac{S_c x + S_t}{x}
B = \frac{9\Phi d\eta}{2\rho_{H_2O} r^2 g}\;\frac{S_c x + S_t}{x}
Per x>0 questa è una curva sempre positiva, monotona decrescente, non presenta minimi, come si può facilmente verificare facendone la derivata:
\frac{\partial B}{\partial t} = -\frac{9\Phi d\eta}{2\rho_{H_2O}r^2 g}\;\frac{S_t}{x^2}
Che non si annulla per nessun valore di x.

 

Mannaggia, non esiste una velocità alla quale conviene correre per bagnarsi il meno possibile,
tuttavia poiché la curva è monotona decrescente, più si aumenta la velocità, meno ci si bagna. Esiste però un valore asintotico, quindi
un valore minimo di acqua, che anche correndo alla velocità della luce, ci prendiamo ugualmente:
\lim_{x\rightarrow \infty}B(x) = \frac{9\Phi d \eta}{2\rho_{H_2O}r^2g}S_c = B_{min}
Definendo il fattore di inzuppamento di un temporale come la quantità I = B/d, possiamo classificare i temporali in base a quanti
litri d’acqua ci colpiscono come minimo per ogni metro che percorriamo!
I = \frac{B_{min}}{d}= \frac{9\Phi \eta}{2\rho_{H_2O}r^2g}S_c
Considerando una persona di statura media (alto 1.8 metri) e in sovrappeso (largo 0.5 metri), otteniamo un ordine di grandezza ragionevole
per S_c:
S_c \approx 0.9 m^2
Ricordiamo inoltre che il flusso di pioggia \Phi dipende dalle dimensioni delle goccie e dalla loro rapidità:
\Phi = n\frac{4}{3}\pi r^3 v_p
Esplicitando anche la dipendenza di vp dal raggio vediamo che \Phi ed r non sono grandezze indipendenti:
\Phi = n\frac{8 \pi\rho g r^5}{27\eta}

Non sappiamo dire se n ed r siano grandezze indipendenti, probabilmente non lo sono, tuttavia per fare un ragionamento per ordini di grandezze supponiamo che n (numero delle goccie di pioggia per unità di volume) sia costante per i vari acquazzoni:
\Phi \propto r^5

Per fare un ragionamento usando gli ordini di grandezza supponiamo che tutto l’aumento di \Phi sia dovuto ad aumento di r, da questo
possiamo, fissati \Phi ed r per la pioggerellina lieve, ricavare tutti i valori di $r$ per gli altri tipi di pioggia noto \Phi.
In seguito è riportata una tabella con i valori del fattore d’inzuppamento per le varie tipologie di pioggia:

tabella

Vediamo come varia il fattore di inzuppamento se consideriamo invece velocità umane, per questo viene riportato un grafico del
fattore di inzuppamento al variare della nostra velocità, usando i dati relativi alle diverse tipologie di temporale.

DifferentiPioggie

Esiste tuttavia come si vede una velocità a cui conviene correre indipendentemente dal tipo di nubifragio, infatti come mostrato nei grafici rinormalizzati, hanno tutti la stessa forma funzionale, e differiscono praticamente solo per costanti moltiplicative.

Rinormalizzato

Insomma, conviene sempre correre alla velocità di 4-5 metri al secondo (intorno ai 20 km/h), per ridurre l’inzuppata!

La matematica dei panini al prosciutto

Posted on by

La matematica dei panini al prosciutto

Tutti sono abituati a pensare alla matematica con teoremi dalle formule incomprensibili e nomi impronunciabili, pure astrazioni accademiche che c’entrano poco con la vita quotidiana . Ma non è proprio cosi. Infatti spesso l’istruzione scolastica tralascia alcuni degli aspetti più simpatici e concreti della matematica, teoremi pensati per risolvere problemi quotidiani con un pizzico della perversione tipica dei matematici. Quanti di voi hanno sentito parlare del teorema dei Carabinieri, di quello della palla pelosa, o il teorema dei matrimoni o quello del panino al prosciutto?

No, non è una presa in giro, esistono tutti veramente e riguardano, più o meno, la vita quotidiana.

Alcuni di questi sono semplicemente nomi scherzosi di problemi strettamente matematici, come il teorema dei carabinieri che riguarda le successioni numeriche: Se una successione (il ladro) si trova tra due successioni (i carabinieri) che convergono ad un unico punto, allora non c’è scampo, anche il ladro convergerà in quel punto e sarà catturato.

Se avete intensione di sposarvi un giorno, fareste bene a conoscere il teorema di Hall, detto anche teorema dei matrimoni.

È un risultato che riguarda gli insiemi e il calcolo combinatorio, ma può facilmente essere espresso così: prendiamo due insiemi, le donne che vivono in Italia e tutti gli uomini che piacciono alle donne italiane.

Riusciranno tutte a sposare l’uomo dei propri sogni se, e solo se il numero di questi uomini è maggiore o uguale del numero delle donne.

E la conseguenza è intuitiva. Più preferenze ha una donna, maggiori sono le possibilità che sposi un uomo che le piace, per cui ragazze, ampliate la vostra lista dei desideri se non volete restare senza marito!

Se mai aveste bisogno di pettinare una palla pelosa dovete sapere che c’è un teorema che dimostra l’impossibilità di pettinarla con regolarità. Per cui se vi capita di avere indomabili vertigini dei capelli, sappiate che la responsabilità è tutta di questo teorema. Applicato al moto dei venti il teorema della palla pelosa afferma che c’è sempre almeno un ciclone sulla Terra. In fondo uragani e vertigini dei capelli hanno molto in comune!

Ora immaginate di fare un bel pic-nic su un prato, siete in due, però avete un solo panino col prosciutto. Con un pizzico di perversione potreste chiedervi se è possibile tagliare il panino esattamente a metà: Il teorema del panino al prosciutto ci dice che è possibile.

Certo, il suo enunciato matematico è piuttosto astruso (Dati n volumi allineati, è sempre possibile costruire un iper-piano che bisezioni tutti gli n volumi), ma questo serve per poter estendere il concetto in spazi a qualunque dimensione.

Se mai vi venisse in mente di farvi un picnic in uno spazio a 5 o 6 dimensioni ora sapete come dividere il cibo con i vostri amici.

Nel caso delle due dimensioni questo teorema cambia nome e diventa il teorema delle frittelle. È sempre possibile costruire una retta che tagli in due parti con pari superficie due forme bidimensionali, in parole povere esiste sempre il modo di dividere due frittelle a metà con un solo taglio dritto.

Mi raccomando, la prossima volta che studiate matematica, panini e frittelle nel piatto e …

buon appetito.