Il super-cattivo di turno vuole escogitare un piano per distruggere il nostro pianeta, uccidendo tutte le forme di vita!
Vuole trovare un modo per disperdere l’atmosfera terrestre nello spazio, lasciando letteralmente “senza fiato” tutte le specie viventi sulla Terra.
Ma come può fare? L’atmosfera sembra ingabbiata dalla forza gravitazionale, che la
tiene ben incollata sulla superficie; bisogna trovare un modo per liberarla!

Esplosione del pianeta Namek
(tratto da qui)
Un gas normalmente tende sempre ad espandersi occupando il massimo volume possibile, perché l’atmosfera non fugge via?
Per nostra fortuna raramente i super-cattivi conoscono bene la Fisica: andiamo
a scoprire come fa la Terra ad intrappolare l’atmosfera!
Immaginiamo di sezionare l’atmosfera in tanti gusci sferici, di spessore .
Su ciascuno di essi agisce la gravità del pianeta:
Dove è la massa di gas atmosferico contenuto nel guscio sferico,
è la
massa della terra e è la distanza del guscio dal centro del nostro pianeta.
La massa del guscio sferico è pari al numero di molecole contenute nel guscio,
ossia la differenza tra le molecole contenute in una sfera di raggio e
una di raggio :
Dove è la massa della singola molecola (supponiamo che il gas atmosferico sia fatto interamente di un tipo di molecola).
Dalla definizione di derivata si ottiene che:
Da cui la forza esercitata sul guscio sferico è pari a:
Assumiamo di studiare un’atmosfera in equilibrio, la forza che agisce sul guscio
deve essere bilanciata dalla pressione esercitata dalle superfici esterne del
guscio:
Dove è la superficie del guscio, moltiplicata per la differenza di pressione tra superficie superiore e inferiore del guscio.
Sostituendo la forza ottenuta:
Da cui otteniamo:
Questa relazione ci lega il numero di molecole con la pressione. Dobbiamo scrivere almeno un’altra relazione, come l’equazione di stato del gas perfetto:
Nel guscio sferico:
Il volume è quello del guscio ():
Adesso però abbiamo di mezzo anche la temperatura. Serve l’ultima relazione
che leghi pressione, temperatura e densità di particelle.
Supponiamo che la nostra atmosfera sia adiabatica, ovvero che ciascun guscio possa salire di quota o scendere di quota senza scambiare calore con l’esterno, mantenendo l’atmosfera in equilibrio.
In tal caso ciascun guscio deve anche rispettare la legge adiabatica:
Dove è una generica costante.
Ricaviamo e sostituiamolo nella prima equazione:
Chiamiamo tutte le costanti per semplicità:
E risolviamo l’equazione differenziale in :
L’integrale si estende a partire dal raggio terrestre (dove la pressione è quella sulla nostra terra pari a 1 atm),
fino alla quota (distanza dal centro della terra, che si troverà a pressione
.
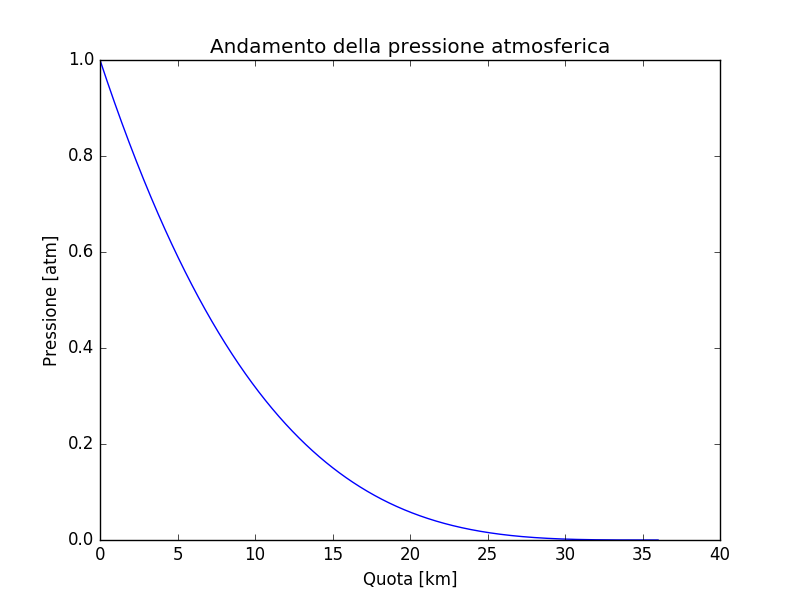
Da cui abbiamo ricavato come varia la pressione atmosferica al variare dell’altitudine. L’atmosfera continua ad esistere solo fin quando l’argomento dentro la radice rimane positivo.
Bisogna solo determinare la costante ; ricordiamo come l’abbiamo definita:
può essere determinato unendo la legge dell’adiabatica con quella del gas perfetto:
Poiché questa relazione vale per qualunque valore di sfruttiamola per
pari al raggio terrestre, dove la temperatura è quella dell’ambiente (circa 300 K che corrispondono a 27 gradi celsius).
Dalla relazione precedente inoltre si può ricavare facilmente anche l’andamento in temperatura in funzione della distanza.
Da cui possiamo ricavare nuovamente la formula per imponendo che l’atmosfera cessi di esistere a quando la temperatura diventa dello zero assoluto.
Vediamo che esiste una condizione per cui l’atmosfera non può più essere contenuta entro un raggio massimo, e quindi fugge via dal pianeta, lasciandolo
arido e deserto:
Se la disuguaglianza è soddisfatta l’atmosfera può esistere.
Cioè esiste un rapporto tra massa del pianeta e temperatura sulla sua superficie che è critico per la formazione di un atmosfera:
Sostituendo i dati della terra si può vedere facilmente che questo limite è rispettato abbondantemente!
Dove abbiamo considerato l’atmosfera interamente composta da molecole di azoto biatomiche (che compongono la maggioranza dell’atmosfera).
Insomma per far fuggire l’atmosfera terrestre un cattivo dovrebbe riscaldarla fino a temperature molto maggiori della temperatura del nucleo del sole! Be direi che se qualcuno riuscisse a fare una bomba così potente, la fuga dell’atmosfera sarebbe l’ultimo dei nostri problemi.
Questo modello è in realtà estremamente semplicistico per descrivere l’atmosfera terrestre per via dell’ipotesi di adiabaticità. La temperatura è descritta correttamente entro una distanza dalla superficie terrestre pari ai primi 15 chilometri di altezza, mentre la pressione è predetta correttamente anche per altezze superiori.
Oltre queste altezza diventano determinanti effetti di riscaldamento atmosferico per l’assorbimento delle radiazioni provenienti dal sole e dallo spazio, che non
abbiamo considerato.
Questo calcolo predice un’atmosfera alta 36 circa km per la terra, che è proprio l’altezza dell’ozono.
In seguito sono mostrati i dati sperimentali ottenuti con un pallone aereostatico per la temperatura, confrontati con le predizioni del modello:
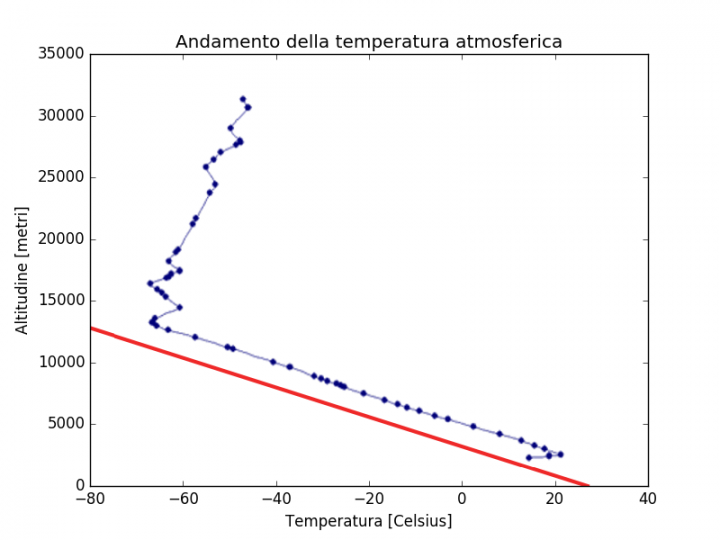
Andamento della temperatura predetto dal modello, confrontato con dei dati sperimentali ottenuti attraverso un pallone aereostatico. I dati NON sono fittati, ma è riportata in rosso la previsione teorica esatta.
I dati originali sono disponibile sul sito web Exploring Earth.
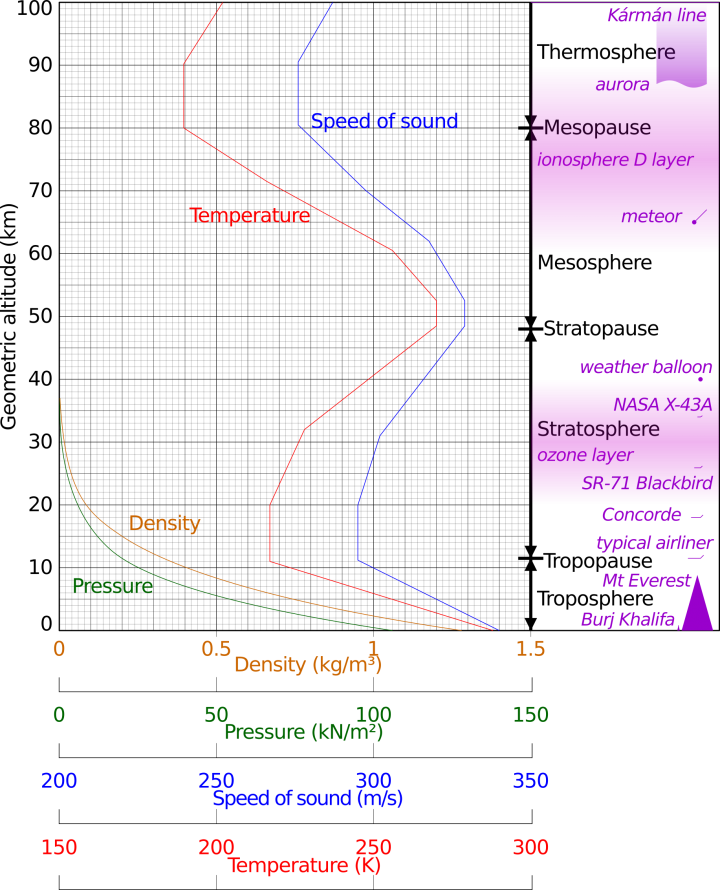
Andamento di pressione, densità, temperatura e velocità del suono nell’atmosfera.
Tratto da Wikipedia.
By Cmglee – Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=17311330
Come mostrato, anche un modellino semplice come questo è in grado di fare previsioni estremamente accurate riguardo all’atmosfera terrestre.