Tag Archives: prede

Lotta per la sopravvivenza

Posted on by

Il ciclo della vita.

La dinamica degli ecosistemi è uno degli argomenti più interessanti, in cui la fisica può essere applicata con successo per studiare l’evoluzione delle popolazioni di prede e predatori.

 

Supponiamo che nel nostro ecosistema ci siano solo due specie in lotta per la sopravvivenza: i pesci (le prede) e gli squali (i predatori).

I pesci hanno a disposizione risorse di cibo praticamente illimitate, se lasciate proliferare si moltiplicano molto rapidamente.

Viceversa gli scquali si cibano solo di pesci, la loro fonte di cibo è quindi molto più scarseggiante, e una sovrappopolazione di predatori causera la loro estinzione per mancanza di cibo. Con una simpatica simulazione è possibile visualizzare la dinamica.

In questa simulazione i quadratini verdi rappresentano i pesci, che si moltiplicano rapidamente, in rosso gli squali, se mangiano pesci si riproducono, altrimenti muoino. Ecco qui un video simpatico che mostra questo ecosistema in azione:

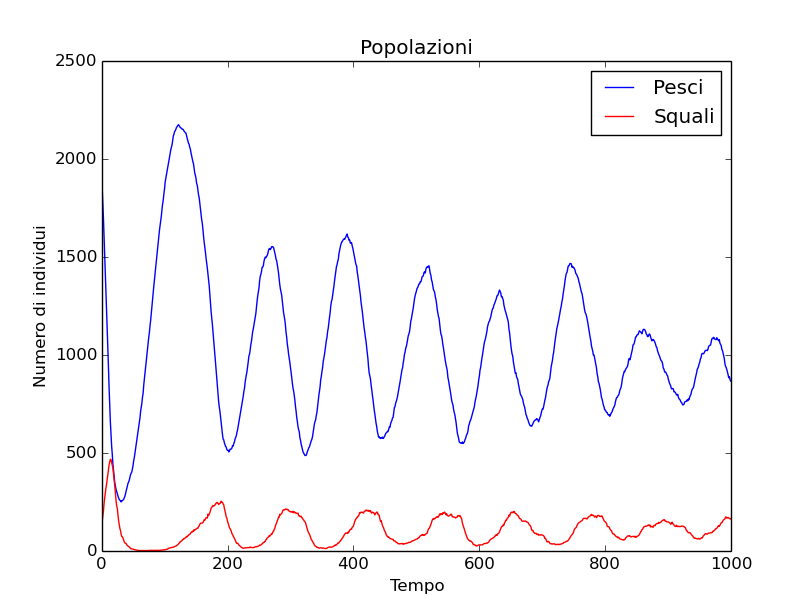
Come si può osservare in numero di pesci e squali aumenta e dinimuisce periodicamente. Se riportiamo su un grafico il numero di prede e quello di predatori notiamo molto bene questo comportamento:

 

Prede e predatori

Prede e predatori

La fisica può descrivere questo tipo di ecosistemi? Si!
Il numero di pesci all’interno del reticolo lo indichiamo con n, il numero di scquali con u.

Scriviamo un’equazione che descriva il comportamento medio di squali e pesci: la probabilità di un pesce di generare un figlio è costante (\alpha), mentre la probabilità che venga mangiata è proporzionale alla probabilità che nei paraggi ci sia uno squalo (\beta).

 
\displaystyle \dot n = n\left(\alpha - \beta u\right)
 
Allo stesso modo la probabilità di uno squalo di generare un figlio è tanto maggiore quanto più alta è la probabilità di incrociare un pesce (\gamma), ma hanno una probabilità costante di morire (\delta):

\displaystyle \dot u = u\left(\gamma n - \delta\right)
 
Queste equazioni (dette di Lotka-Volterra in onore dei due matematici che le formularono per primi) non hanno soluzione analitica, tuttavia con un cambio di variabili possiamo riscriverle in modo da poterne dare un’interpretazione fisica:
 
\displaystyle p = \ln n \qquad q = \ln u

\displaystyle \dot p = \frac{\dot n}{n} \qquad \dot q = \frac{\dot u}{u}
 

Con questa sostituzione il sistema di equazioni che descrive il comportamento medio dei nostri “pesciolini” è:
 
\displaystyle \left\{\begin{array}{l} \dot p = \alpha - \beta e^q \\ \dot q = \gamma e^p - \delta \end{array}\right.
 

Queste due equazioni differenziali adesso descrivono un sistema hamiltoniano canonico:
 
\displaystyle \left\{\begin{array}{l} \displaystyle \dot p = -\frac{\partial H}{\partial q}\\ \\ \displaystyle \dot q = \frac{\partial H}{\partial p} \end{array}\right.
 

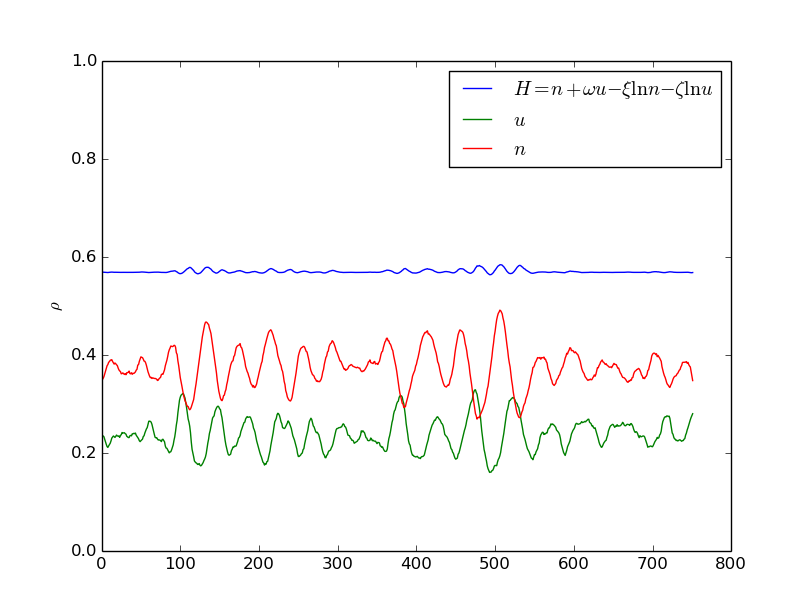
Si può facilmente ricavare l’hamiltoniana di questo sistema:
 
\displaystyle H = -\alpha q -\delta p + \beta e^q + \gamma e^p
 

Quindi è possibile definire un “energia” dell’ecosistema, che è in media conservata (ricordiamoci che le equazioni che abbiamo scritto valgono in media, non tengono conto di piccole fluttuazioni locali della popolazione).
Risostituendo le variabili originali otteniamo che l’energia del sistema é:
 
\displaystyle H = \beta u + \gamma n - \alpha \ln u - \delta \ln n
 
Se il numero di pesci e squali è molto alto questo implica che la loro somma, pesata sui coefficienti \beta e \gamma si conserva.

\beta era la probabilità che, data un interazione tra preda e predatore, la preda muoia, mentre \gamma è la probabilità che, data un’interazione tra predatore abbia il sopravvento e quanto questa interazione sia favorevole alla sua procreazione.

Se dividiamo tutto per \beta otteniamo:
\displaystyle H' \approx u + \frac{\gamma}{\beta} n

Dove adesso \frac{\gamma}{\beta} è un coefficiente che tiene conto di quanto influenza il cibarsi dei predatori sulla loro crescita. La condizione \gamma = \beta vuol dire che ogni volta che un predatore acchiappa la preda, fa anche un figlio.

Questa condizione tuttavia è molto difficile da raggiungere in pratica, ecco la stima dei parametri per
una delle simulazioni effettuate:
 

\displaystyle \omega = \frac{\gamma}{\beta} \qquad \xi = \frac{\alpha}{\beta} \qquad \zeta = \frac{\delta}{\beta}
 

I valori ottenuti numericamente dalla simulazione sono:
\displaystyle \omega \approx 0.29 \qquad \xi \approx 0.36 \qquad \zeta \approx 0.069

Come si può vedere il modello di Lotka-Volterra descrive molto bene l’andamento che è stato misurato.
Conservazione